Angular Momentum Of A System Of Particles
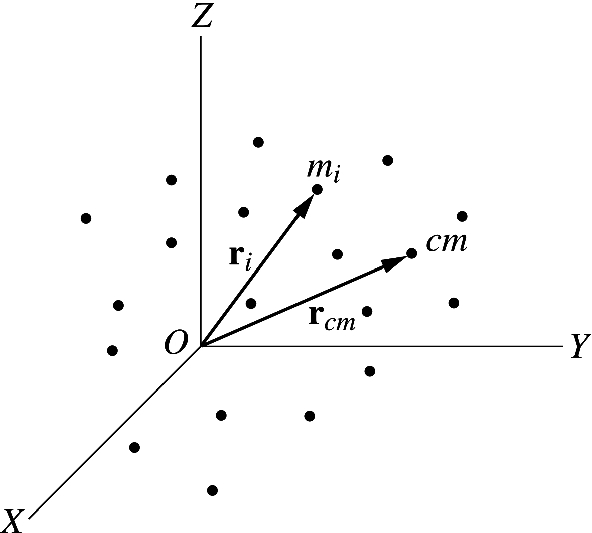
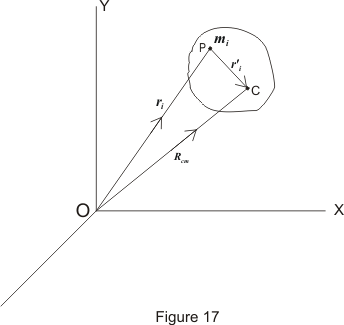
Angular momentum of a system of particles. R0 i ri R where dRdt 0 because we are efiecting an instantaneous shift in the axes. Hence p0 i pi and J 0 X i ri pi. It is explained as below.
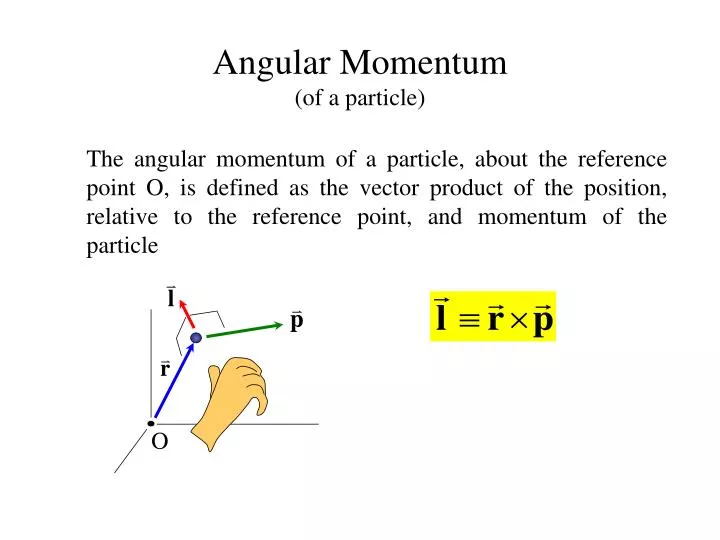
DV dt is the acceleration of the centre of mass. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. The angular momentum mathbf L of a system of particles about a fixed point is the vector sum of angular momenta of the individual particles.
The total angular momentum of a system of such structureless point particles is then the vector sum L X X r p 52. S L. B Show that if the total force on a system of particles is zero the torque on the system is the same about all origins.
Conservation of Angular Momentum about a Fixed Point O The angular momentum of a system of particles about a fixed point O is the sum of the angular momentum of the individual particles n H O r i m iv i. S j L S j. As a result of the angular momentum-angular position indeterminacy its angular position must be completely indeterminate.
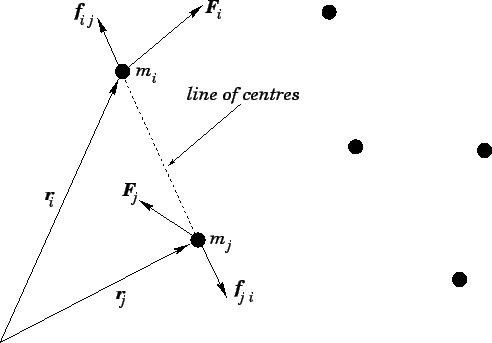
S j r. Also the force is attractive so its an attractive inverse-square law force which can also be determined using. 192 Angular Momentum about a Point for a Particle 1921 Angular Momentum for a Point Particle Consider a point-like particle of mass m moving with a velocity v Figure 191.
Differentiate the above equation. But the sum on the right side is just the total linear momentum of all the particles. X i ri Rpi.
X i ri. The individual stars can be treated as point particles each of which has its own angular momentum.
The individual stars can be treated as point particles each of which has its own angular momentum.
S j. Solving for this we find an important result. The total momentum of a system is the same as if all the particles were located. J I ω constant In our case external torque is acting then angular momentum is not conserved. S j. Now we know that l r p so. R The angular momentum. The individual stars can be treated as point particles each of which has its own angular momentum. Angular momentum of a system of particles to angular momentum of the systems center of mass.
Angular Momentum one h2π two h2π three h2π. Angular momentum of a multi-component system Consider a system consisting of mutually interacting point particles. DV dt is the acceleration of the centre of mass. As a result we may state that a system of particles total linear momentum is equal to the product of the systems total mass and the velocity of its Centre of mass. Yes the angular momentum of a system of particles is conserved. A new system of axes. The change in the angular momentum of the system of particles about a point S is given by.

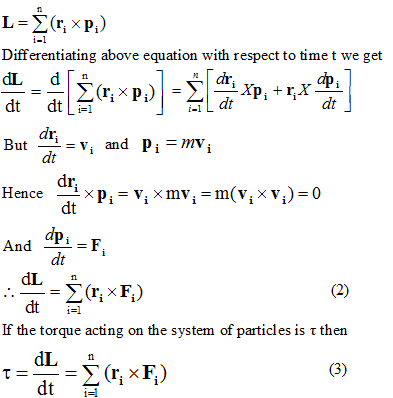

































Post a Comment for "Angular Momentum Of A System Of Particles"